Local variable selection in a varying coefficient regression model
One important thing to note about a varying coefficient regression (VCR) model is that the coefficients vary over the model’s domain. It seems natural, then, that the set of relevant predictors might vary over the domain, as well. This post is about local adaptive grouped regularization (LAGR), which is a method of local variable selection in a VCR model.
#How it works
##Local polynomial regression To begin, assume that the coefficients are smooth functions of the location parameter $s$. At any location in the domain, the coefficients can be approximated as locally linear:
##Adaptive group lasso The adaptive group lasso is used to penalize the coefficient $\beta(s)$ and its slope $\nabla \beta(s)$ simultaneously. The local coefficient can be shrunk all the way to zero is the penalty is large enough. This accomplishes local variable selection.
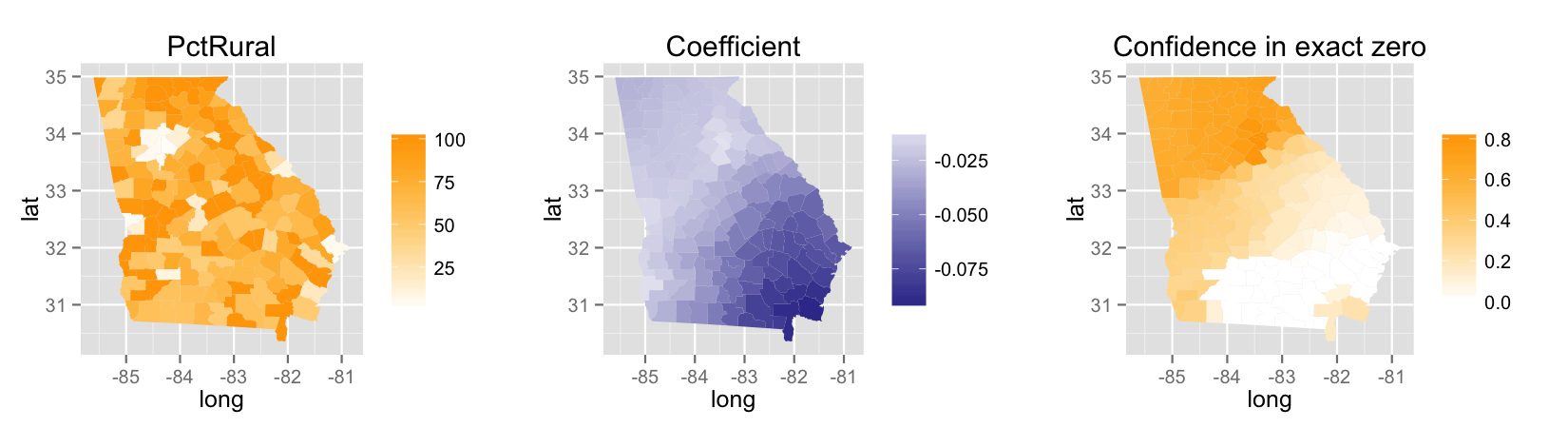
##Example The data for this example has to do with demographics in Georgia, aggregated to the county level. The data is from the 1990 US Census. We are estimating the associations between educational attainment and some other demographic covariates. Educational attainment is measured as the percentage of a county’s residents who have at least a bachelor’s degree. Below, I’ve plotted the estimated association of educational attainment with the percentage of a county’s residents who are rural.